The Odd Chopsticks Problem
Recently, I moved house, and took the opportunity to unpack all the things I had in storage. Among them were my chopsticks.
But there was a problem. While I have six of everything else — bowls, plates, cups, etc. — I have an odd number of chopsticks: 13. To make things worse, three are from a different set.
So I have
- Five pairs of chopsticks the same length
- One pair of a longer length
- And one spare chopstick, of the longer length
What do I do? Do I discard one chopstick, leaving six pairs? Discard three, leaving an awkward five pairs? Or throw the whole lot away and start again?
Aesthetically, the best thing to do would be to chuck them all. Chopsticks are a dime a dozen (not literally, but almost). But that seems wasteful.
Logically, the best thing to do would be to discard one chopstick and keep six pairs, despite one pair being of a different length. But that presented an interesting problem: What would be the likelihood of getting an odd pair of chopsticks?
Time for some high school math (or maths, to my antipodean compatriots).
The Odd Chopsticks Pair Probability
To calculate the probability of an odd pair of chopsticks, I’ll first count all possible pairings.
The number of pairs in a set can be determined by c = n! / (2! * (n-2)!). In this case, n is 12. This formula gives 66 possible pairs. Seems about right.
But how many of these are odd pairs? The number of pairs of items from sets a and b is simply a * b. I don’t need any fancy math. It’s 2 * 10 or 20.
That means the possibility of picking one long and one short chopstick is 20/66, or 0.303 or 30.3%.
Analysis: That’s too high! Roughly one in three times I go get a pair of chopsticks, I’d get a mismatched pair. And the possibility would be even higher if I kept three of the longer ones in there (about 38%).
But 30.3% seems weird. Is my math correct? I aced stats in uni, but that was decades ago. We still used calculators! (Do people still? I have no idea.)
To try and figure out if I was right, I went to Google Sheets.
For column A, I created a random number from 1 to 12. This is with randbetween:
=randbetween(1,12)Easy peasy.
Now, for column A, I need a random number from 1 to 12 other than the value in column A. Not so easy!
To do this, I’ll use a combination of
sequencewhich creates a sequence of numbersfilterwhich will remove the value in the first column, andindex(randbetween)to choose the value in the remaining range.
So for the value in A2, I use:
=INDEX(FILTER(SEQUENCE(12,1,1), SEQUENCE(12,1,1) <> A2), RANDBETWEEN(1, 11))I can safely hardcode 11 because I know that when you remove a value from a 12-number array, you get 11 values.
OK, so what do we get?
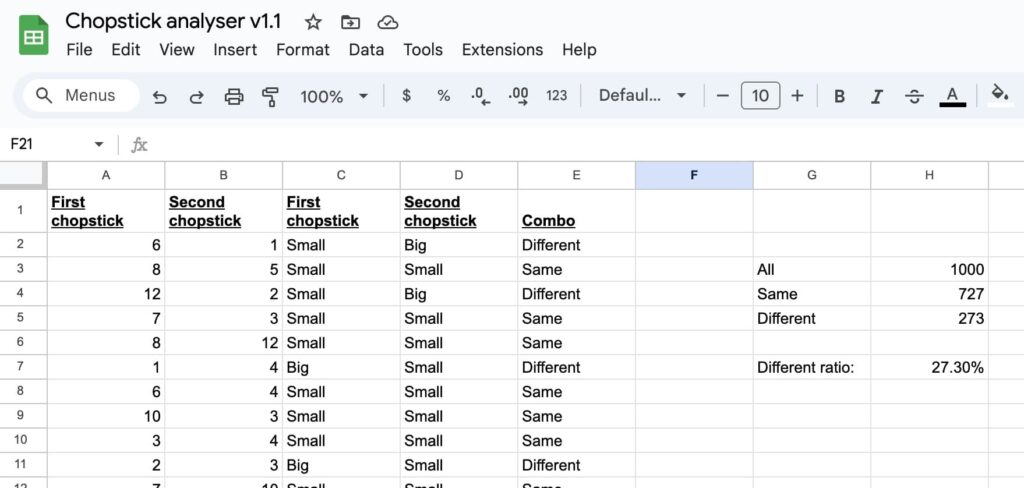
What?? 27.3%?? Is 1000 rows not enough? Or is my math terrible?
Double Checking
I actually went back first and checked my math again. Could I be so far off? I decided to try it a different way. The number of pairs in an unordered set would normally be be 12 x 11.
But because these are symmetrical pairs (i.e. it doesn’t matter which is chopstick one or chopstick two), I divide that by two. The result is the same as with the fancy factorials above: 66 possible combinations of chopsticks.
OK fine, let’s do a 50,000 row spreadsheet.
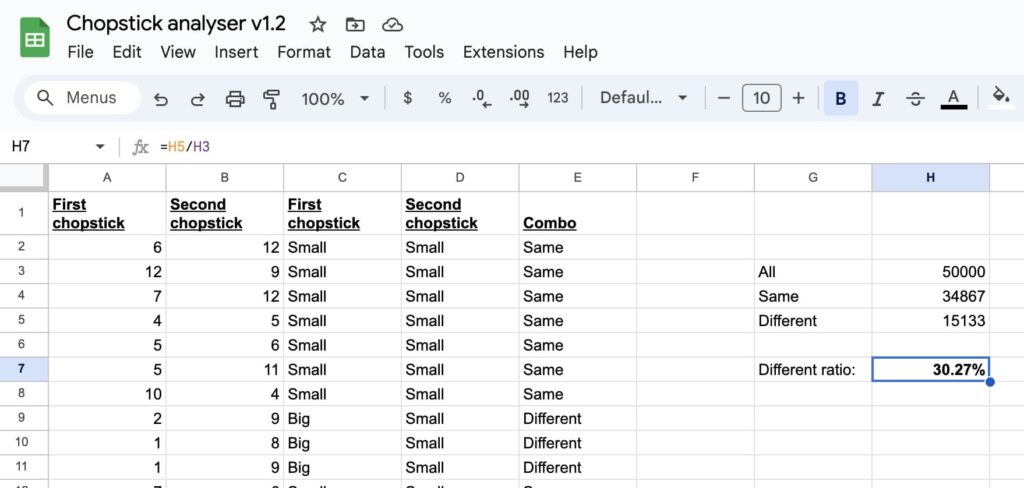
Now we’re cooking. 30.27% seems close enough to show I’m right.
So, it seems like the best logical outcome is to discard the extra chopsticks. Right?
The Actual Answer
Upon presenting this to my partner, she told me that she had actually purchased that set of ten chopsticks. It was never meant to be a set of twelve. Asian cultures aren’t as obsessed with dozens and half-dozens as Commonwealth cultures are.
And despite all this, my brother offered a nugget of wisdom: Tie the extra two chopsticks together so they aren’t accidentally pulled out with the rest. When the need arises, give that last pair to the sixth guest.
Chopsticks problem solved. If you’ve read it this far, I think we’d be friends…







This article is hilarious. Entertaining the whole way through. But what’s the name of your brother who came up with that brilliant suggestion at the end? He sounds so smart, and handsome, probably.